Practice Questions
1. Use Euclid’s division lemma to show that the square of any positive integer is either of form 3m or 3m + 1 for some integer m.
[Hint: Let x be any positive integer then it is of the form 3q, 3q + 1 or 3q + 2. Now square each of these and show that they can be rewritten in the form 3m or 3m + 1.]
Ans. Let a be any positive integer and b = 3.
Then a = 3q + r for some integer q ≥ 0
And r = 0, 1, 2 because 0 ≤ r < 3
Therefore, a = 3q or 3q + 1 or 3q + 2
Or,
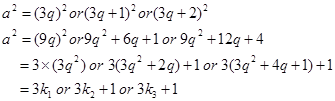
Where k1, k2, and k3 are some positive integers
Hence, it can be said that the square of any positive integer is either of the form 3m or 3m + 1.
2. Express each number as product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Ans. (i) 140 = 2 ´ 2 ´ 5 ´ 7 = 22´ 5 ´ 7
(ii) 156 = 2 ´ 2 ´ 3 ´ 13 = 22´ 3 ´ 13
(iii) 3825 = 3 ´ 3 ´ 5 ´ 5 ´ 17 = 32´ 52´ 17
(iv) 5005 = 5 ´ 7 ´ 11 ´ 13
(v) 7429 = 17 ´ 19 ´ 23
3. Given that HCF (306, 657) = 9, find LCM (306, 657).
Ans. HCF (306, 657) = 9
We know that, LCM × HCF = Product of two numbers
\ LCM × HCF =306 × 657
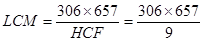
LCM = 22338
4. Check whether 6n can end with the digit 0 for any natural number n.
Ans. If any number ends with the digit 0, it should be divisible by 10.
In other words, it will also be divisible by 2 and 5 as 10 = 2 × 5
Prime factorisation of 6n = (2 ×3)n
It can be observed that 5 is not in the prime factorisation of 6n.
Hence, for any value of n, 6n will not be divisible by 5.
Therefore, 6n cannot end with the digit 0 for any natural number n.
5. Prove that (3+2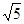
) is irrational.
Ans. We will prove this by contradiction.
Let us suppose that (3+2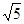) is rational.
It means that we have co-prime integers a and b (b≠0) such that
⇒ 
⇒ 
⇒ 
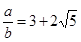
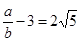
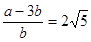
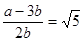… (1)
a and b are integers.
It means L.H.S of (1) is rational but we know that 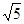is irrational. It is not possible. Therefore, our supposition is wrong. (3+2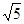) cannot be rational.
Hence, (3+2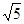) is irrational.
Practice Questions
1. Use Euclid’s division lemma to show that the square of any positive integer is either of form 3m or 3m + 1 for some integer m.
[Hint: Let x be any positive integer then it is of the form 3q, 3q + 1 or 3q + 2. Now square each of these and show that they can be rewritten in the form 3m or 3m + 1.]
Ans. Let a be any positive integer and b = 3.
Then a = 3q + r for some integer q ≥ 0
And r = 0, 1, 2 because 0 ≤ r < 3
Therefore, a = 3q or 3q + 1 or 3q + 2
Or,
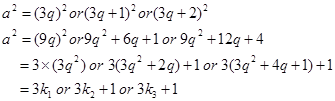
Where k1, k2, and k3 are some positive integers
Hence, it can be said that the square of any positive integer is either of the form 3m or 3m + 1.
2. Express each number as product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Ans. (i) 140 = 2 ´ 2 ´ 5 ´ 7 = 22´ 5 ´ 7
(ii) 156 = 2 ´ 2 ´ 3 ´ 13 = 22´ 3 ´ 13
(iii) 3825 = 3 ´ 3 ´ 5 ´ 5 ´ 17 = 32´ 52´ 17
(iv) 5005 = 5 ´ 7 ´ 11 ´ 13
(v) 7429 = 17 ´ 19 ´ 23
3. Given that HCF (306, 657) = 9, find LCM (306, 657).
Ans. HCF (306, 657) = 9
We know that, LCM × HCF = Product of two numbers
\ LCM × HCF =306 × 657
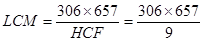
LCM = 22338
4. Check whether 6n can end with the digit 0 for any natural number n.
Ans. If any number ends with the digit 0, it should be divisible by 10.
In other words, it will also be divisible by 2 and 5 as 10 = 2 × 5
Prime factorisation of 6n = (2 ×3)n
It can be observed that 5 is not in the prime factorisation of 6n.
Hence, for any value of n, 6n will not be divisible by 5.
Therefore, 6n cannot end with the digit 0 for any natural number n.
5. Prove that (3+2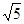) is irrational.
Ans. We will prove this by contradiction.
Let us suppose that (3+2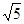) is rational.
It means that we have co-prime integers a and b (b≠0) such that
⇒
⇒
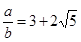
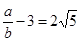
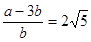
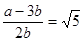⇒ … (1)
a and b are integers.
It means L.H.S of (1) is rational but we know that 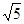is irrational. It is not possible. Therefore, our supposition is wrong. (3+2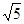) cannot be rational.
Hence, (3+2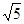) is irrational.
6. 
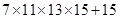is a
(a) Composite number
(b) Whole number
(c) Prime number
(d) None of these
Ans. (a)and(b)both
7. For what least value of ‘n’ a natural number,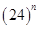 
is divisible by 8?
(a) 0
(b) -1
(c) 1
(d) No value of ‘n’ is possible
Ans. (c) 1
8. The sum of a rational and an irrational number is
(a) Rational
(b) Irrational
(c) Both (a) & (c)
(d) Either (a) or (b)
Ans. (b) Irrational
9. HCF of two numbers is 113, their LCM is 56952. If one number is 904, then other number is:
(a) 7719
(b) 7119
(c) 7791
(d) 7911
Ans. (b) 7119
10. A lemma is an axiom used for proving
(a) other statement
(b) no statement
(c) contradictory statement
(d) none of these
Ans. a) other statement
11. If HCF of two numbers is 1, the two numbers are called relatively ________ or ________.
(a) prime, co-prime
(b) composite, prime
(c) Both (a) and (b)
(d) None of these
Ans. (a) prime, co-prime
12. 
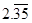is
(a) a terminating decimal number
(b) a rational number
(c) an irrational number
(d) Both (a) and (b)
Ans. (b) a rational number
13. 2.13113111311113……is
(a) a rational number
(b) a non-terminating decimal number
(c) an irrational number
(d) Both (a) & (c)
Ans. (c) an irrational number
14. The smallest composite number is:
(a) 1
(b) 2
(c) 3
(d) 4
Ans. (c) 3
15. 
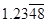is
(a) an integer
(b) an irrational number
(c) a rational number
(d) None of these
Ans. (c) a rational number
16. 
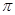is
(a) a rational number
(b) an irrational number
(c) both (a) & (b)
(d) neither rational nor irrational
Ans. (b) an irrational number
17. (2+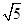
) is
(a) a rational number
(b) an irrational number
(c) an integer
(d) not real number
Ans. (b) an irrational number