 |
| CBSE Previous Year Questions: Real Numbers |
Q.1. Find a rational number between √2 and √3. [Delhi 2019]
Ans: Let p be rational number between √2 and √3
√2 = 1.41
√3 = 1.73
On squaring throughout, we have
2 < p2 < 3
The perfect squares which lie between 2 and 3 are 2 < 2.25 < 2.56 < 2.89 < 3.
Taking square root throughout
The rational numbers between √2 and √3 are 1.5, 1.6, 1.7 and more.
Q.2. Prove that √2 is an irrational number. [Delhi 2019]
Ans: Let us assume that √2 is a rational number.
So it can be expressed in the form p/q where p, q are co-prime integers and q ≠ 0
√2 = p/q
Here p and q are coprime numbers and q ≠ 0
√2 = p/q
On squaring both the sides we get,
=> 2 = (p/q)2
=> 2q2 = p2……………………………..(1)
p2/2 = q2
So 2 divides p and p is a multiple of 2.
⇒ p = 2m
⇒ p2 = 4m2 ………………………………..(2)
From equations (1) and (2), we get,
2q2 = 4m2
⇒ q2 = 2m2
⇒ q2 is a multiple of 2
⇒ q is a multiple of 2
Hence, p, q have a common factor 2. This contradicts our assumption that they are co-primes. Therefore, p/q is not a rational number
√2 is an irrational number.
Q.3. Prove that 2 + 5 √3 is an irrational number, given that √3 is an irrational number. [CBSE, Allahabad 2019]
Ans: Let 2 + 5 √3 be a rational number. (p and q are co-prime positive integers, q ≠ 0)
∴
⇒
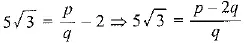
which is a contradiction because √3 is an irrational number and
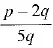is a rational.Q.4. The HCF of two numbers a and b is 5 and their LCM is 200. Find the product ab. [CBSE 20 19 (30/5/2)]
Ans: The formula that shows the relation between LCM and HCF of a and b is: LCM (a, b) = (a × b) / HCF (a, b)
HCF (a, b) = 5, and LCM (a, b) = 200
LCM (a, b) = (a × b) / HCF (a, b)
200 = (a × b) / 5
a × b = 200 × 5
a × b = 1000
Therefore, the product of 'a' and 'b' is 1000.
Q.5. A number N when divided by 14 gives the remainder 5. What is the remainder when the same number is divided by 7? [CBSE 2019 (30/2/1)]
Ans: Let the number be X
Since dividing the number gives remainder as 5, X can be written as 14 * Y + 5
where Y will be the quotient on dividing X by 14.
X = 14 * Y + 5
X = 2 * 7 * Y + 5
Let's divide both sides by 7 (since we want to know the remainder when X is divided by 7)
X/7 = (2 * 7 * Y)/7 + 5/7
X/7 = 2 * Y + 5/7
Since Y is a whole number (quotient), thus 2 * Y will also be a whole number and what remains is 5/7.
Thus, the remainder is 5 when X is divided by 7.
Q.6. Find after how many places the decimal form o f the number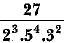
will terminate. [CBSE 2019 (30/3/3)
Ans: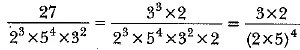 
So, the decimal form will end after four decimal places.
Q.7. Express 429 as product of its prime factors. [CBSE 2019 (30/3/3)]
Ans:
∴ 429 = 3 x 13 x 11
Q.8. Find the HCF of 612 and 1314 using prime factorisation. [CBSE 2019 (30/5/3)]
Ans:
612 = 2 x 2 x 3 x 3 x 17
1314 = 2 x 3 x 3 x 73
HCF = 2 x 3 x 3 = 18
Q.9. Find the HCF o f 1260 and 7344 using Euclid’s algorithm.
[NCERT, CBSE 2019 (30/1/1)]
OR
Use Euclid’s division algorithm to find the HCF of 255 and 867.
[CBSE 2019 (30/4/1)]
Ans: Since 7344 > 1260 and from Euclid’s algorithm
a = bq + r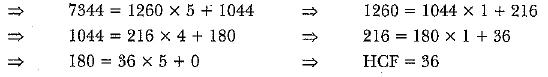
OR
Solution is similar as above.
Only values are changed
Q.10. Write a rational number between √2 and √3. [CBSE 2019 (30/1/2)]
Ans: A rational number between √2 and √3 is √2.89 = 1.7 = 17/10.
Q.11. If HCF of 65 and 117 is expressible in the form 65n - 117, find the value of n. [CBSE 2019 (30/3/3)]
Ans: HCF (65, 117) is given by
65 = 5 x 13
117 = 13 x 3 x 3
⇒ HCF =13
According to question,
65n - 117 = 13
65n = 130
n = 2
Q.12. Write the smallest number which is divisible by both 306 and 657.
[CBSE 2019 (30/2/1)]
Ans: Here, to find the required smallest number we will find LCM of 306 and 657.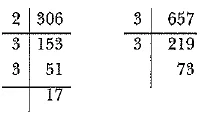
306 = 2 x 32 x 17
657 = 32 x 73
LCM - 2 X 32 x 17 x 73 = 22338
Q.13. Show that any positive odd integer is of the form 6q + 1 or 6q + 3 or 6q + 5 where q is some integer.
[NCERT]
OR
Show that any positive odd integer is of the form 6 m + 1 or 6 m + 3 or 6 m + 5, where m is some integer. [CBSE 2019(30/5/2)]
Ans: Let a be any positive odd integer and b = 6. Then, by Euclid's algorithm, a = 6q + r, for some integer q > 0 and 0 < r < 6.
i.e., the possible remainders are 0, 1, 2, 3, 4, 5.
Thus, a can be of the form 6q or 6q + 1 or 6q + 2 or 6q + 3 or 6q + 4 or 6q + 5, where q is some quotient.
Since a is odd integer, so a cannot be of the form 6q or x 6q + 2 or 6q + 4 (since they are even).
Thus, a is of the form 6q + 1 or 6q + 3 or 6q + 5, where q is some integer.
Hence, any odd positive integer is of the form 6q + 1 or 6q + 3 or 6q + 5, where q is some integer.
OR
Let a be any positive odd integer and b = 6. Then, by Euclid’s algorithm, a = 6m + r, for some integer m > 0 and 0 < r < 6.
i.e., the possible remainders are 0, 1, 2, 3, 4, 5.
Thus, a can be of the form 6m, or 6m + 1 or 6m + 2 or 6m + 3 or 6m + 4 or 6m + 5, where m is some quotient.
Since a is odd integer, so a cannot be of the form 6m or 6m + 2 or 6m + 4 (since they are even). Thus, a is of the form 6m + 1, 6m + 3 or 6m + 5, where m is some integer.
Hence, any odd positive integer is of the form 6m + 1 or 6m + 3 or 6m + 5, where m is some integer.
Q.14. Find HCF and LCM of 404 and 96 and verify that HCF x LCM = Product of the two given numbers. [CBSE 2018]
Ans: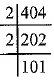
HCF of 404 and 9
404 = 2 x 2 x 101
96 = 2 x 2 x 2 x 2 x 2 x 3
Common factor = 2 x 2 = 4
∴ HCF = 4
LCM of 404 and 96
= 2 x 2 x 101 x 2x 2x 2 x 3 = 9696
Verification:
HCF x LCM = 4 x 9696 = 38784
Product of two numbers = 404 x 96 = 38784
Clearly, HCF x LCM = Product of two numbers
Hence verified
Q.15. Write whether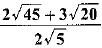 
on simplification gives an irrational or a rational number. [CBSE 2018 (C)]
Ans: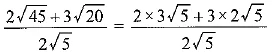 
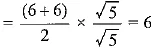(rational number)
Q.16. What is the HCF of smallest prime number and the smallest composite number? [CBSE 2018]
Ans: Prime number: A prime number is a number that has exactly two factors i.e. it can be divided by only the number ‘1’ and itself.
The smallest prime number is = 2
Composite number: A composite number has more than two factors, which means apart from getting divided by number 1 and itself, it can also be divided by at least one integer or number. We don’t consider the number ‘1’ as a composite number.
The smallest composite number is = 4
2 is the factor of 4
∴ H.C.F of the smallest prime number and the smallest composite number is 2.
Q.17. Given that √2 is irrational, prove that (5 + 3 √2 ) is an irrational number [CBSE 2018]
Ans: Let 5 + 3 √2 = p/q be a rational number, where p and q, have no common factor other than 1 and q ≠ 0.
⇒ 
For any values of p and q(q ≠ 0), RHS =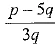 
is rational, but LHS = √2 is s irrational.
This contradicts the fact. So, our assumption is wrong.
∴ 5 + 3 √2 is an irrational number.
Q.18. Given that √3 is an irrational number, prove that (2 + √3 ) is an irrational number. [CBSE 2018 (C)]
Ans: Let (2 + √3 is not an irrational.
∴ it can be written in the form a/b, where b ≠ 0 and a and b are coprime.
So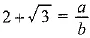 
Subtracting 2 from both sides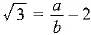
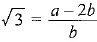This contradicts.
LHS is an irrational number because √3 is an irrational number (given) and RHS is an rational number.
So, LHS is equal to RHS not possible.
Hence, our assumption is wrong.
∴ (2 + √3 is an irrational number.
Q.19. What is the HCF of the smallest composite number and the smallest prime number? [CBSE 2018]
Ans: The smallest prime number is 2.
The smallest composite number is 4.
To find the HCF of 2 and 4 let us write their prime factorization.
2 = 2
4 = 2 × 2
HCF (2, 4) = 2
Thus, the HCF of the smallest composite number and the smallest prime number is 2.
Ans: Let us assume, to the contrary, that Vs is a rational number.
Then, there exist co-prime positive integers a and b such that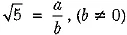
So, a = √5 b
Squaring both sides, we have
a2 = 5b2 ......(i)
⇒ 5 divides a2 ⇒ 5 divides a
So, we can write
a = 5c (where c is any integer)
Putting the value of a = 5c in (i), we have
25c2 = 5b2 => 5c2 = b2
It means 5 divides b2 and so 5 divides b.
So, 5 is a common factor of both a and b which is a contradiction.
So, our assumption that √5 is a rational number is wrong.
Hence, we conclude that √5 is an irrational number.
