We know that according to the law of conservation of energy in a closed system, i.e., a system that is isolated from its surroundings, the total energy of the system is conserved”. Conservative force abides by the law of conservation of energy. In this article, let us understand and learn about conservative and non-conservative forces.
A comparative study between Non-Conservative and Conservative force
In this article let us study in brief about two types of forces namely conservative forces and non-conservative forces. Let us also know the comparison between conservative force and non-conservative force.
Consider the following two situations as shown in the figure.
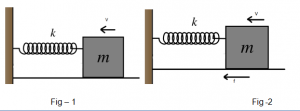
In figure 1, when the mass comes to rest, the spring gets compressed by a distance of ‘x’. The spring then comes to its normal length and mass attains a velocity ‘v’. This compression and elongation continue each time with a maximum value of ‘x’. So we can infer that the total mechanical energy of the system (Block + Spring) remains constant. While in the second case also there will be compression and elongation but the minimum value will keep on decreasing. So we can say that the total mechanical energy of the system is not conserved in this case.
From our observations in the above case, we can now define conservative and non-conservative forces. A conservative force is a force that does zero work done in a closed path. If only these forces act then the mechanical energy of the system remains conserved. Conservative force abides by the law of conservation of energy.
Examples of conservative force: Gravitational force, spring force etc.
On the other hand, non-conservative forces are those forces which cause a loss of mechanical energy from the system. In the above case friction is the non-conservative force. But as we know energy can neither be created nor destroyed hence these forces convert mechanical energy into heat, sound, light etc.
Examples of non-conservative forces are Friction, Air Resistance, and Tension in the cord.
Now, Conservative force has one more property that work done by it is independent of the path taken.
Work Done By a Conservative Force
Consider the following scenario
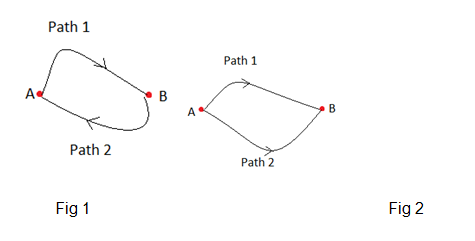
Work done by the conservative force in a closed path is zero.
In figure (1) we know work done by the conservative force in a closed path is zero.
W1, A, B + W2, B, A = 0
W1, A, B = – W2, B, A
We also have,
W2, B, A = – W2, A, B
Using the above two equations we get,
W1, A, B = W2, A, B
The above equation shows that work done to move a particle from point A to B through path 1 and 2 as shown in figure 2 will take the same amount of work done. But this statement is not valid for non-conservative forces.
Difference Between Conservative Force and Non-conservative Force
| Conservative Force | Non-Conservative Force |
| W1 = W2 | W1 ≠ W2 |
| For closed path: W = 0 | For closed path: W ≠ 0 |
| The force is independent of the path. | The force depends on the path. |
| Gravitational Force, Spring Force, and Electrostatic force between two electric charges are examples of conservative force. | Friction, Air resistance, and Tension in the cord are examples of non-conservative force. |
Conservative force formula
Conservative force is defined as the force such that the work done is independent of the path taken and is dependent only on the initial and final position. Conservative force is applied to the law of conservation of energy. The basic understanding of conservation of energy holds good for conservation of kinetic energy and is given as:
Frequently Asked Questions – FAQs
State true or false: A force is said to be conservative if the work done over any closed path is zero.
State law of conservation of energy.
The law of conservation of energy states that “In a closed system, i.e., a system that is isolated from its surroundings, the total energy of the system is conserved.”
Give two examples to explain the law of conservation of energy.
Examples of conservation of energy are:
- In a generator, mechanical energy is converted into electrical energy.
- In a loudspeaker, electrical energy is converted into sound energy.