Basic Proportionality Theorem & It's Proof - Goyanka Maths Study

• State BPT theorem and prove it.

Hint: To prove this theorem first we will join BE and CD. Then draw a line EL perpendicular to AB and line DM perpendicular to AC. Now we will find the ratio of area of Δ$\mathrm{\Delta }$ADE to Δ$\mathrm{\Delta }$DBE and ratio of area of Δ$\mathrm{\Delta }$ADE to Δ$\mathrm{\Delta }$ECD. Comparing the ratios we will get the final answer.

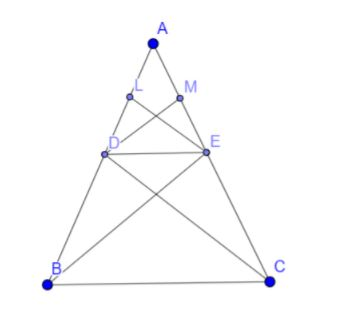
Complete step-by-step answer:

Now, ΔDBE$\mathrm{\Delta }DBE$ and ΔECD$\mathrm{\Delta }ECD$ being on the same base DE and between the same parallels DE and BC, we have,ar(ΔDBE)=ar(ΔECD)$ar(\mathrm{\Delta }DBE)=ar(\mathrm{\Delta }ECD)$ then we say that the basic proportionality theorem is proved.

Basic proportionality theorem:

If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio.

Given:
A ΔABC$\mathrm{\Delta }ABC$in which DE∥BC$DE\parallel BC$and DE intersects AB and AC at D and E respectively.

To prove that:
ADDB=AEEC${\displaystyle \frac{AD}{DB}}={\displaystyle \frac{AE}{EC}}$

Construction:Join BE and CD.

Draw EL⊥AB$EL\mathrm{\perp }AB$and DM⊥AC$DM\mathrm{\perp }AC$

Proof:
We have the
ar(ΔADE)=12×AD×EL$ar(\mathrm{\Delta }ADE)={\displaystyle \frac{1}{2}}\times AD\times EL$
ar(ΔDBE)=12×DB×EL$ar(\mathrm{\Delta }DBE)={\displaystyle \frac{1}{2}}\times DB\times EL$
Therefore the ratio of these two is ar(ΔADE)ar(ΔDBE)=ADDB${\displaystyle \frac{ar(\mathrm{\Delta }ADE)}{ar(\mathrm{\Delta }DBE)}}={\displaystyle \frac{AD}{DB}}$. . . . . . . . . . . . . . (1)
Similarly,
ar(ΔADE)=ar(ΔADE)=12×AE×DM$ar(\mathrm{\Delta }ADE)=ar(\mathrm{\Delta }ADE)={\displaystyle \frac{1}{2}}\times AE\times DM$
ar(ΔECD)=12×EC×DM$ar(\mathrm{\Delta }ECD)={\displaystyle \frac{1}{2}}\times EC\times DM$
Therefore the ratio of these two is ar(ΔADE)ar(ΔECD)=AEEC${\displaystyle \frac{ar(\mathrm{\Delta }ADE)}{ar(\mathrm{\Delta }ECD)}}={\displaystyle \frac{AE}{EC}}$. . . . . . . . . . . .. . . (2)

Now, ΔDBE$\mathrm{\Delta }DBE$ and ΔECD$\mathrm{\Delta }ECD$ being on the same base DE and between the same parallels DE and BC, we have,
ar(ΔDBE)=ar(ΔECD)$ar(\mathrm{\Delta }DBE)=ar(\mathrm{\Delta }ECD)$. . . . . . . . . . . (3)
From equations 1, 2, 3 we can conclude that
ADDB=AEEC${\displaystyle \frac{AD}{DB}}={\displaystyle \frac{AE}{EC}}$
Hence we can say that the basic proportionality theorem is proved.

Note: The formula for area of the triangle is given by 12×b×h${\displaystyle \frac{1}{2}}\times b\times h$where b, h are base and height respectively. If two triangles are on the same base and between the same parallels then the area of those two triangles are equal.

---

Related Questions

Rhombus PQRB is inscribed in △ABC$△ABC$ such that ∠B$\mathrm{\angle }B$ is one of its angles, P, Q and R lie on AB, AC and BC respectively. If AB=12cm$AB=12cm$ and BC=6cm$BC=6cm$, find the sides of rhombus PQRB.

In the following figure LM||CB$LM||CB$and LN||CD$LN||CD$, prove that AMAB=ANAD${\displaystyle \frac{AM}{AB}}={\displaystyle \frac{AN}{AD}}$. $$