अनुपात (Ratio) : अनुपात हमेशा दो सजातीय राशि में होता है। एक राशि का दूसरी राशि में भाग देने पर अनुपात प्राप्त होता है। जैसे यदि A राशि को B राशि से भाग दिया जाये, तब 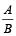 को A तथा B का अनुपात कहते हैं। इसे निम्न प्रकार लिखते हैं :
को A तथा B का अनुपात कहते हैं। इसे निम्न प्रकार लिखते हैं :
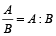
अतः अनुपात A : B में A को प्रथम पद तथा B को द्वितीय पद कहा जाता है। यदि किसी अनुपात के प्रत्येक पद को 0 को छोड़कर किसी निश्चित संख्या से गुणा या भाग करते हैं तो वह अनुपात अपरिवर्तित रहता है।
अनुपात के गुण (Properties of Ratio)
a : b = m a : m b, जहाँ m एक स्थिरांक है।
a : b : c = A : B : C जो समतुल्य है 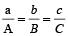 के।
के।
यह एक महत्वपूर्ण गुण है जो तीन राशियों के अनुपात में उपयोग होता है।
यदि 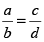 ,
,
तो 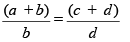
अनुपात का यह गुण कम्पोनेंडो (Componendo) कहलाता है
उदाहरण के लिए : 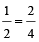
इसलिए, 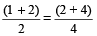
= 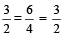
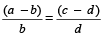
यह गुण डिविडेंडो (Dividendo) कहलाता है।
उदाहरण के लिए: 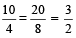
इसलिए, 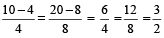
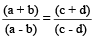
यह गुण कम्पोनेंडो और डिविडेंडो (Componendo and Dividendo) कहलाता है।
उदाहरण के लिए: 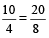
इसलिए, 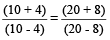 =
= 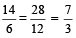
यदि 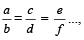
तो 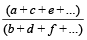 = प्रत्येक का अलग-अलग अनुपात
= प्रत्येक का अलग-अलग अनुपात
उदाहरण के लिए: 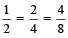
इसलिए 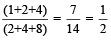
यदि A > B तब 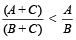 जहाँ A, B और C प्राकृतिक संख्याएँ हैं।
जहाँ A, B और C प्राकृतिक संख्याएँ हैं।
उदाहरण के लिए: 3 > 2,
तब, 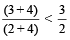 [क्योंकि
[क्योंकि 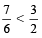 ]
]
यदि A < B
तो 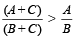
जहाँ A, B और C प्राकृतिक संख्याएँ हैं।
उदाहरण के लिए: 2 < 3,
तब, 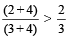 [क्योंकि
[क्योंकि 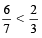 ]
]
एक दी हुई राशि को दिये गये अनुपात में विभाजित करना
माना एक दी हुई राशि ‘a’ को अनुपात m : n में विभाजित करना है।
माना दी हुई राशि का एक भाग x है तो दूसरा भाग a – x होगा।
∴ 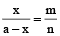
या nx = ma – mx
या (m + n) x = ma
∴ पहला भाग है 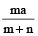
और दूसरा भाग होगा 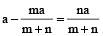
उदाहरण 1. 70 को 3 : 7 अनुपात में विभाजित कीजिए।
हल: माना पहला भाग x है, तो दूसरा भाग = 70 – x
∴ 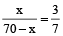
या 7x = 210 – 3x
या x = 21 और 70 – x = 49
अतः 70 के दो अभीष्ट भाग 21 और 49 हैं।
उदाहरण 1. 70 को 3 : 7 अनुपात में विभाजित कीजिए।
हल: माना पहला भाग x है, तो दूसरा भाग = 70 – x
∴ 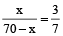
या 7x = 210 – 3x
या x = 21 और 70 – x = 49
अतः 70 के दो अभीष्ट भाग 21 और 49 हैं।
किसी द्विआयामी चित्रों में, यदि भुजाओं का अनुपात x : y हो, तो उनके क्षेत्रफलों का अनुपात x² : y² होगा।
उदाहरण 2. दो वृतों की त्रिज्याओं का अनुपात 2 : 5 है। उनके क्षेत्रफलों का अनुपात ज्ञात करें।
हल: उनके क्षेत्रफलों का अनुपात = 2² : 5² = 4 : 25
किसी त्रिआयामी चित्रों में, यदि भुजाओं का अनुपात x : y हो, तो उनके आयतनों का अनुपात x³ : y³ होगा। यदि दो संख्याओं का अनुपात a : b है और यदि प्रत्येक संख्या में x वृद्धि होने पर अनुपात c : d हो जाए तब, दो संख्याओं का योग
= 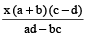
दो संख्याओं का अंतर
= 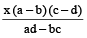
दो दी हुई संख्याएँ हैं
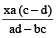 और
और 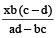
उदाहरण 3. दो संख्याओं का अनुपात 3 : 4 है। यदि प्रत्येक संख्या में 2 की वृद्धि हो, तो अनुपात 7 : 9 हो जाता है। संख्याएँ ज्ञात करें।
हल: संख्याएँ हैं
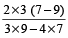 और
और 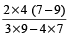
या 12 और 16
निरंतर समानुपात: यदि तीन संख्याएँ a, b और c निरंतर समानुपात में हो, तो हम कह सकते हैं कि a, b और c समानुपात में हैं।
तो, 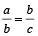
b² = ac ⇒ b =
अतः हम कह सकते हैं कि ‘a’ पहला समानुपात, ‘c’ तीसरा समानुपात और ‘b’ मध्य समानुपात है।
प्रत्यक्ष समानुपात: यदि X, Y के प्रत्यक्ष समानुपाती हो तो किसी एक के बढ़ने या घटने पर दूसरे पर उसका सीधा प्रभाव पड़ेगा। यदि X बढ़ता है तो Y भी बढ़ेगा और यदि X घटता है तो Y भी घटेगा।
व्युत्क्रम समानुपात: यदि X, Y के व्युत्क्रमानुपाती हो यानी दोनों में किसी एक के बढ़ने या घटने पर दूसरे पर उसका व्युत्क्रम प्रभाव पड़ेगा। यदि X के बढ़ने पर Y घटे और X के घटने पर Y बढ़े तो इस समानुपात को व्युत्क्रम समानुपात कहते हैं।
- यदि चार राशियाँ समानुपात में हो तो किनारे की राशियों का गुणनफल, बीच की राशियों के गुणनफल के बराबर होता है।
माना a, b, c, d चार राशियाँ समानुपात में हैं, तो 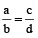
तब ad = bc
- यदि तीन राशियाँ a, b और c निरंतर समानुपात में हो, तो a : b = b : c
तब ac = b²
b मध्य समानुपात कहलाता है।
- यदि तीन राशियाँ समानुपात में हो तो पहली और तीसरी राशि का अनुपात, पहली और दूसरी राशि के अनुपात के समान होता है।
यदि a : b : : b : c तो a : c = a² : b²
मध्य समानुपात ज्ञात करना
उदाहरण 6. 3 और 75 के बीच मध्य समानुपात ज्ञात करें।
हल: माना x अभीष्ट समानुपात है, तो 3 : x : : x : 75
∴ x = 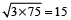
जब चार राशियाँ समानुपात में हो, तो अज्ञात मान ज्ञात करनाः
उदाहरण 7. चार संख्याएँ 10, 18, 22, 38 में प्रत्येक में कौन-सी संख्या जोड़ी जाए कि वे समानुपात में हो जाएँ?
हल: माना कि अभीष्ट संख्या x है प्रश्न के अनुसार, हम पाते हैं
(10 + x) : (18 + x) : : (22 + x) : (38 + x)
⇒ (10 + x) (38 + x) = (18 + x) (22 + x)
⇒ 380 + 48x + x² = 396 + 40x + x²
⇒ 380 + 48x = 396 + 40x
⇒ 48x – 40x = 396 – 380
⇒ 8x = 16
⇒ 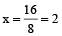
अतः चारों दी हुई संख्याओं में, 2 जोड़ी जानी चाहिए।
चौथा समानुपात ज्ञात करना
उदाहरण 8. p² – pq + q², p³ + q³, p – q का चौथा समानुपात ज्ञात करें।
हल: माना x चौथा समानुपात है
∴ (p²– pq + q²) : (p³ + q³) = (p – q) : x
⇒ (p² – pq + q²) × x = (p³ + q³) (p – q)
∴ 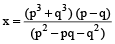
⇒ 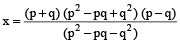
⇒ 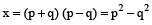
∴ अभीष्ट चौथा समानुपात p² – q² है।
तीसरा समानुपात ज्ञात करना
उदाहरण 9. a² – b² और a + b के बीच तीसरा समानुपात ज्ञात करें।
हल: माना x अभीष्ट तीसरा समानुपात है,
तब, a² – b² : a + b = a + b : X
∴ (a² – b²) x = (a + b) (a + b)
∴ 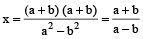

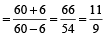
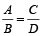 ⇒ A : B : : C : D यहाँ AD = BC
⇒ A : B : : C : D यहाँ AD = BC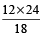 = 16
= 16