PRACTICE QUESTIONS ON BASIC PROPORTIONALITY THEOREM

Question 1 :

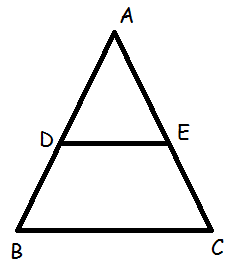
In ΔABC, D and E are points on the sides AB and AC respectively such that DE ∥ BC (i) If AD/DB = 3/4 and AC = 15 cm find AE.

(ii) If AD = 8x −7 , DB = 5x −3 , AE = 4x −3 and EC = 3x −1  find the value of x.

Question 2 :

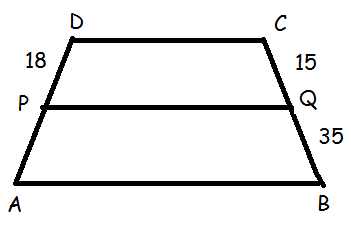
ABCD is a trapezium in which AB || DC and P,Q are points on AD and BC respectively, such that PQ || DC if PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD

Question 3 :

In ΔABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DE ||BC

(i) AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm.

(ii) AB = 5.6 cm, AD = 1.4 cm, AC = 7.2 cm and AE = 1.8 cm.

---

Solutions : 

Question 1 :

In ΔABC, D and E are points on the sides AB and AC respectively such that DE ∥ BC (i) If AD/DB = 3/4 and AC = 15 cm find AE.

Solution :

AD/DB  =  AE/EC

AC  =  15 (Given)

Let AE  =  x and EC  =  15 - x

3/4  =  x/(15-x)

3(15 - x)  =  4x

45 - 3x  =  4x

4x + 3x  =  45

7x  =  45

x  =  45/7

x  =  6.43

(ii) If AD = 8x −7 , DB = 5x −3 , AE = 4x −3 and EC = 3x −1  find the value of x.

Solution :

AD/DB  =  AE/EC

(8x - 7)/(5x - 3)  =  (4x - 3)/(3x - 1)

(8x - 7) (3x - 1)  =  (4x - 3)(5x - 3)

24x² - 8x - 21x + 7  =  20x² - 12x - 15x + 9

24x²-20x² - 29x + 27x + 7 - 9  =  0

4x²- 2x - 2  =  0

2x²- x - 1  =  0

(2x + 1) (x - 1)  =  0

x  =  -1/2 and x = 1

Hence the value of x is 1.

Question 2 :

ABCD is a trapezium in which AB || DC and P,Q are points on AD and BC respectively, such that PQ || DC if PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD

Solution :

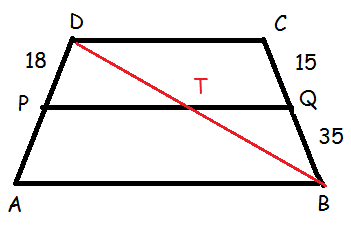
Let us draw the a rough picture based on the given information.

Let us join DB.

In triangle DAB,

PD/PA  =  DT/TB  ----(1)

In triangle DBC, 

BT/TD  =  BQ/QC 

By taking reciprocal on both sides,

TD/BT  =  QC/BQ  ----(2)

(1)  =  (2) 

---

PD/PA  =  QC/BQ  

18/PA  =  15/35

PA  =  18(35)/15

PA  =  42

AD  =  42 + 18

AD  =  60 cm

Question 3 :

In ΔABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DE ||BC

(i) AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm.

Solution :

AD  =  8 AB  =  AD + DB 12  =  8 + DB DB  =  12 - 8 DB  =  4 AC  =  18 AC  =  AE + EC 18  =  12 + EC EC  =  18 - 12 EC  =  6 cm AD/DB  =  AE/EC 8/4  =  12/6 2  =  2 Hence DE ||BC. (ii) AB = 5.6 cm, AD = 1.4 cm, AC = 7.2 cm and AE = 1.8 cm. Solution : AD  =  1.4 AB  =  AD + DB 5.6  =  1.4 + DB DB  =  5.6 - 1.4 DB  =  4 .2 cm AC  =  7.2 AC  =  AE + EC 7.2  =  1.8 + EC EC  =  7.2-1.8 EC  =  5.4 cm AD/DB  =  AE/EC 1.4/4.2  =  1.8/5.4 0.33  =  0.33 Hence DE ||BC.