Check case study questions released by CBSE for Class 10 Maths Chapter 6 - Triangles. Solve these questions to prepare the case study questions for the CBSE Class 10 Maths Exam 2021-22.
CBSE Class 10 Maths Case Study Questions for Chapter 6 - Triangles are available here. Students must practice with these questions to perform well in their Maths exam. All these case study questions have been published by the Central Board of Secondary Education (CBSE). For the convenience of students, all the questions are provided with answers.
Case Study Questions for Class 10 Maths Chapter 6 - Triangles
CASE STUDY 1:
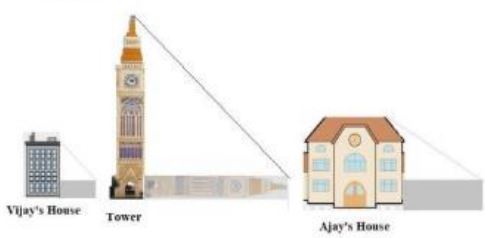
Vijay is trying to find the average height of a tower near his house. He is using the properties of similar triangles.The height of Vijay’s house if 20m when Vijay’s house casts a shadow 10m long on the ground. At the same time, the tower casts a shadow 50m long on the ground and the house of Ajay casts 20m shadow on the ground.
1. What is the height of the tower?
a) 20m
b) 50m
c) 100m
d) 200m
Answer: c) 100m
2. What will be the length of the shadow of the tower when Vijay’s house casts a shadow of 12m?
a) 75m
b) 50m
c) 45m
d) 60m
Answer: d) 60m
3. What is the height of Ajay’s house?
a) 30m
b) 40m
c) 50m
d) 20m
Answer: b) 40m
4. When the tower casts a shadow of 40m, same time what will be the length of the shadow of Ajay’s house?
a) 16m
b) 32m
c) 20m
d) 8m
Answer: a) 16m
5. When the tower casts a shadow of 40m, same time what will be the length of the shadow of Vijay’s house?
a) 15m
b) 32m
c) 16m
d) 8m
Answer: d) 8m
CASE STUDY 2:
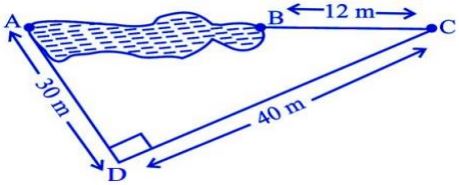
Rohan wants to measure the distance of a pond during the visit to his native. He marks points A and B on the opposite edges of a pond as shown in the figure below. To find the distance between the points, he makes a right-angled triangle using rope connecting B with another point C are a distance of 12m, connecting C to point D at a distance of 40m from point C and the connecting D to the point A which is are a distance of 30m from D such the ∠ADC=900.
1. Which property of geometry will be used to find the distance AC?
a) Similarity of triangles
b) Thales Theorem
c) Pythagoras Theorem
d) Area of similar triangles
Answer: c)Pythagoras Theorem
2. What is the distance AC?
a) 50m
b) 12m
c) 100m
d) 70m
Answer: a) 50m
3. Which is the following does not form a Pythagoras triplet?
a) (7, 24, 25)
b) (15, 8, 17)
c) (5, 12, 13)
d) (21, 20, 28)
Answer: d) (21, 20, 28)
4. Find the length AB?
a) 12m
b) 38m
c) 50m
d) 100m
Answer: b) 38m
5. Find the length of the rope used.
a) 120m
b) 70m
c) 82m
d) 22m
Answer: c)82m
SCALE FACTOR
Case study:
A scale drawing of an object is the same shape at the object but a different size. The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The scale is written as a ratio. The ratio of two corresponding sides in similar figures is called the scale factor
Scale factor= length in image / corresponding length in object
If one shape can become another using revising, then the shapes are similar. Hence, two shapes are similar when one can become the other after a resize, flip, slide or turn. In the photograph below showing the side view of a train engine. Scale factor is 1:200
This means that a length of 1 cm on the photograph above corresponds to a length of 200cm or 2 m, of the actual engine. The scale can also be written as the ratio of two lengths.
1. If the length of the model is 11cm, then the overall length of the engine in the photograph above, including the couplings (mechanism used to connect) is:
a) 22cm
b) 220cm
c) 220m
d) 22m
Answer: a)22m
2. What will affect the similarity of any two polygons?
a) They are flipped horizontally
b) They are dilated by a scale factor
c) They are translated down
d) They are not the mirror image of one another.
Answer: d)They are not the mirror image of one another
3. What is the actual width of the door if the width of the door in photograph is 0.35cm?
a) 0.7m
b) 0.7cm
c) 0.07cm
d) 0.07m
Answer: a)0.7m
4. If two similar triangles have a scale factor 5:3 which statement regarding the two triangles is true?
a) The ratio of their perimeters is 15:1
b) Their altitudes have a ratio 25:15
c) Their medians have a ratio 10:4
d) Their angle bisectors have a ratio 11:5
Answer: b)Their altitudes have a ratio 25:15
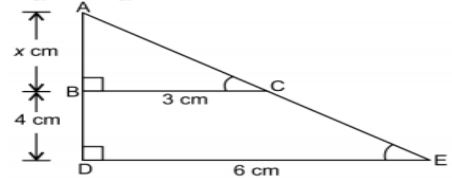
5. The length of AB in the given figure:
a) 8cm
b) 6cm
c) 4cm
d) 10cm
Answer: c)4cm
Also Check: