Free PDF Download of CBSE Maths Multiple Choice Questions for Class 12 with Answers Chapter 1 Relations and Functions. Maths MCQs for Class 12 Chapter Wise with Answers PDF Download was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 12 Maths Relations and Functions MCQs Pdf with Answers to know their preparation level.
Relations and Functions Class 12 Maths MCQs Pdf
1. Let R be a relation on the set L of lines defined by l1 R l2 if l1 is perpendicular to l2, then relation R is
(a) reflexive and symmetric
(b) symmetric and transitive
(c) equivalence relation
(d) symmetric
Answer/Explanation
Answer: d
Explaination: (d), not reflexive, as l1 R l2
⇒ l1 ⊥ l1 Not true
Symmetric, true as l1 R l2 ⇒ l2R h
Transitive, false as l1 R l2, l2 R l3
⇒ l1 || l3 . l1 R l2.
2. Given triangles with sides T1 : 3, 4, 5; T2 : 5, 12, 13; T3 : 6, 8, 10; T4 : 4, 7, 9 and a relation R in set of triangles defined as R = {(Δ1, Δ2) : Δ1 is similar to Δ2}. Which triangles belong to the same equivalence class?
(a) T1 and T2
(b) T2 and T3
(c) T1 and T3
(d) T1 and T4
Answer/Explanation
Answer: c
Explaination: (c), T1 and T3 are similar as their sides are proportional.
3. Given set A ={1, 2, 3} and a relation R = {(1, 2), (2, 1)}, the relation R will be
(a) reflexive if (1, 1) is added
(b) symmetric if (2, 3) is added
(c) transitive if (1, 1) is added
(d) symmetric if (3, 2) is added
Answer/Explanation
Answer: c
Explaination: (c), here (1,2) e R, (2,1) € R, if transitive (1,1) should belong to R.
4. Given set A = {a, b, c). An identity relation in set A is
(a) R = {(a, b), (a, c)}
(b) R = {(a, a), (b, b), (c, c)}
(c) R = {(a, a), (b, b), (c, c), (a, c)}
(d) R= {(c, a), (b, a), (a, a)}
Answer/Explanation
Answer: b
Explaination: (b), A relation R is an identity relation in set A if for all a ∈ A, (a, a) ∈ R.
5. A relation S in the set of real numbers is defined as xSy ⇒ x – y+ √3 is an irrational number, then relation S is
(a) reflexive
(b) reflexive and symmetric
(c) transitive
(d) symmetric and transitive
Answer/Explanation
Answer: a
Explaination:
6. Set A has 3 elements and the set B has 4 elements. Then the number of injective functions that can be defined from set A to set B is
(a) 144
(b) 12
(c) 24
(d) 64
Answer/Explanation
Answer: c
Explaination: (c), total injective mappings/functions
= 4 P3 = 4! = 24.
7. Given a function lf as f(x) = 5x + 4, x ∈ R. If g : R → R is inverse of function ‘f then
(a) g(x) = 4x + 5
(b) g(x) =
(c) g(x) =
(d) g(x) = 5x – 4
Answer/Explanation
Answer: c
Explaination: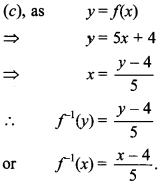
8. Let Z be the set of integers and R be a relation defined in Z such that aRb if (a – b) is divisible by 5. Then R partitions the set Z into ______ pairwise disjoint subsets.
Answer/Explanation
Answer:
Explaination: Five, as remainder can be 0, 1, 2, 3, 4.
9. Consider set A = {1, 2, 3 } and the relation R= {(1, 2)}, then? is a transitive relation. State true or false.
Answer/Explanation
Answer:
Explaination: True, as there is no situation
(a, b) ∈ R, (b, c) ∈ R Hence, transitive. We can also say, a relation containing only one element is transitive.
10. Every relation which is symmetric and transitive is reflexive also. State true or false.
Answer/Explanation
Answer:
Explaination: False,e.g.if R is arelationinset A = {2,3,4} defined as {(2, 3), (3, 2), (2, 2)} is symmetric and transitive but not reflexive.
11. Let R be a relation in set N, given by R = {(a, b): a = b – 2, b > 6} then (3, 8) ∈ R. State true or false with reason.
Answer/Explanation
Answer:
Explaination: False, as in (3, 8), b = 8
⇒ a = 8 – 2
⇒ a = 6, but here a = 3.
12. Let R be a relation defined as R = {(x, x), (y, y), (z, z), (x, z)} in set A = {x, y, z} then R is (reflexive/symmetric) relation.
Answer/Explanation
Answer:
Explaination: Reflexive, as for all a ∈ A, (a, a) ∈ R.
13. Let R be a relation in the set of natural numbers N defined by R = {(a, b) ∈ N × N: a < b}. Is relation R reflexive? Give a reason.
Answer/Explanation
Answer:
Explaination:
Given R = {(a, b) ∈ N × N: a < b}.
Not reflexive, as for (a, a) × R
⇒ a< a, not true.
14. Let A be any non-empty set and P(A) be the power set of A. A relation R defined on P(A) by X R Y ⇔ X ∩ Y = X, X, Y ∈ P(A). Examine whether ? is symmetric.
Answer/Explanation
Answer:
Explaination: X R Y ⇔ X ∩ Y = X ⇒ Y ∩ X = X ⇒ Y R X.
Hence, symmetric.
15. State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive. [NCERT; Delhi 2011]
Answer/Explanation
Answer:
Explaination: (1, 2) ∈ R, (2, 1) ∈ R, but (1, 1) ∉ R.
16. Show that the relation R in the set {1,2,3} given by R = {(1,1), (2, 2), (3, 3), (1, 2), (2, 3)} is reflexive but neither symmetric nor transitive. [NGERT]
Answer/Explanation
Answer:
Explaination:
Given R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} defined on R: {1, 2, 3} → {1, 2, 3}
For reflexive: As (1, 1), (2,2), (3, 3) ∈ R. Hence, reflexive
For symmetric: (1, 2) ∈ R but (2, 1) ∉ R. Hence, not symmetric.
For transitive: (1, 2) ∈ R and (2, 3) ∈R but (1, 3) ∉ R. Hence, not transitive.
17. Let A = {3, 4, 5} and relation R on set A is defined as R = {(a, b) e A x A : a – b – 10). Is relation an empty relation?
Answer/Explanation
Answer:
Explaination: We notice for no value of a, b s A, a-b = 10. Hence, (a, b) £ R for a, b e A. Hence, empty relation.
18. Given set A = {a, b} and relation R on A is defined as R = {(a, a), (b, b)}. Is relation an identity relation?
Answer/Explanation
Answer:
Explaination: Yes, as (a, a) ∈ R, for all a ∈ A..
19. Let set A represents the set of all the girls of a particular class. Relation R on A is defined as R = {(a, b) ∈ A × A : difference between weights of a and b is less than 30 kg}. Show that relation R is a universal relation.
Answer/Explanation
Answer:
Explaination: Let a, b ∈ A then a – b < 30 kg, always true for students of a particular class, i.e. aRb ∀ a, b ∈ A. Hence, universal relation.
20. If A = {1, 2, 3} and relation R = {(2, 3)} in A. Check whether relation R is reflexive, symmetric and transitive.
Answer/Explanation
Answer:
Explaination:
Not reflexive, as (1, 1) ∉ R.
Not symmetric, as (2, 3) ∈ R but (3,2) ∉ R.
Transitive, as relation R in a non empty set containing one element is transitive.
21. State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive. [Delhi]
Answer/Explanation
Answer:
Explaination: As (1, 2) ∈ R, (2, 1) ∈ R, but (1, 1) ∉ R.
22. Consider the set A containing n elements, then the total number of injective functions from set A onto itself is _____ .
Answer/Explanation
Answer:
Explaination: Total number of injective functions from set containing n elements to a set containing n elements is n Pn = n!
23. The domain of the function f : R → R defined by f(x) = is ______ .
Answer/Explanation
Answer:
Explaination:
[-2, 2]. For domain 4 – x² ≥ 0
⇒ 4 ≥ x²
⇒ x² ≤ 4
⇒ x² ≤ (2)²
⇒ -2 ≤ x ≤ 2, i.e. [-2, 2].
24. Let A = {a, b }. Then number of one-one functions from A to A possible are
(a) 2
(b) 4
(c) 1
(d) 3
Answer/Explanation
Answer:
Explaination: (a), as if n(A) = m, then possible one-one functions from A to A are m!
25. Let A = {1, 2, 3, 4} and B = {a, b, c}. Then number of one-one functions from A to B are ______.
Answer/Explanation
Answer:
Explaination: 0, as n(A) > n(B)
26. If n(A) = p, then number of bijective functions from set A to A are ______ ..
Answer/Explanation
Answer:
Explaination: p!, as for bijective functions from A to B, n(A) = n(B) and function is one-one onto.
27. The function f : R → R defined as f(x) = [x], where [x] is greatest integer ≤ x, is onto function. State true or false.
Answer/Explanation
Answer:
Explaination: False, as range of f is set of integers, i.e.
Z and range of f ⊆ co-domain R. Hence,not onto e.g. for ∈ R (co-domain) there is no x ∈ R (domain) such that y = f(x) or e∈ R has no pre-image.
28. If \(f(x)=\frac{x-1}{|x-1|}, x(\neq 1) \in R\) then range of ‘f’ is _______ .
Answer/Explanation
Answer:
Explaination: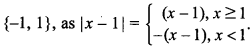
29. If f : R → R be defined by f(x) = (3 – x3)1/3, then find fof(x). [NCERT]
Answer/Explanation
Answer:
Explaination: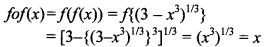
30. If f is an invertible function defined as f(x) = , write f-1(x).
Answer/Explanation
Answer:
Explaination: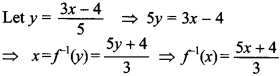
31. Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. State whether f is one-one or not. [AI 2011] f
Answer/Explanation
Answer:
Explaination: One-one, as for x1 ≠ x2
⇒ f(x1) ≠ f(x2).
32. Let f : R → R is defined by f (x) = | x |. Is function f onto? Give a reason. [HOTS]
Answer/Explanation
Answer:
Explaination: f is not onto, as for some y ∈ R from co-domain, there is no x ∈ R from domain such that y = f(x), e.g. for -2 ∈ R (co-domain) there is no x ∈ R (domain) such that f(x) = -2, i.e. |x| = -2. Hence, not onto.
33. If f : R → R and g : R → R are given by f (x) = sin x and g(x) = 5x², find gof(x).
Answer/Explanation
Answer:
Explaination: gof(x) = g(f(x)) = g(sin x) = 5 sin² x.
34. Let f : {1, 3,4} → {1,2, 5} and g: {1,2, 5} → {1, 3} be given by f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}. Write down gof. [NCERT]
Answer/Explanation
Answer:
Explaination:
gof: {1, 3, 4} → {1, 3}.
gof(1) = g(f(1)) = g(2) = 3.
gof(3) = g(K3)) = g(5) = 1
gof(4) = g(f(4)) = g(1) = 3
gof = {(1, 3), (3, 1), (4, 3)}.
35. Prove that f : R → R given by f(x) = x3 + 1 is one-one function.
Answer/Explanation
Answer:
Explaination:
Given f(x) = x3 + 1
For x1 ≠ x2
⇒ x13 ≠ x23
⇒ x13 + 1 ≠ x23 + 1
⇒ f(x1) ≠ f(x2). Hence, one-one
36. Show that the Signum Function f : R → R,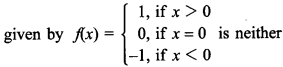
one-one nor onto.
Answer/Explanation
Answer:
Explaination:
Range of function is {-1, 0, 1} and co-domain is set of real numbers R.
⇒ Range ⊆ co-domain.
There is at least one element in R(codomain) which is not image of any element of the domain, e.g. for 2 e R(co-domain), there is no x in domain such that f(x) = 2, x ∈ R.
Hence, function is not onto.
Also, let x1 = 2 and x2 = 3 then f(x1) = 1 and f(x2) = 1
i.e., x1 ≠ x2 ⇒ f(x1) = f(x2).
So, function is not one-one.
37. Given f(x) = sin x check if function f is one-one for (i) (0, π) (ii) (-, ).
Answer/Explanation
Answer:
Explaination:
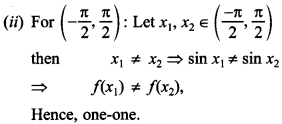
38. If f : R → R is defined by f(x) = 3x + 2, define f (f(x)). [Foreign]
Answer/Explanation
Answer:
Explaination: f(f(x)) = f(3x + 2) = 3(3x + 2) + 2
= 9x+ 8.
39. Write fog, if f : R → R and g : R → R are given by f(x) = |x| and g(x) = |5x – 2|. [Foreign]
Answer/Explanation
Answer:
Explaination: (fog)(x) =f(g(x))
=f(|5x-2|) = ||5x-2||.
40. Write fog, if f : R → R and g : R → R are given by f(x) = 8x3 and g(x) = x1/3. [Foreign]
Answer/Explanation
Answer:
Explaination: (fog)(x) = f(g(x)) = f(x1/3) = 8(x1/3)3 = 8x.
We hope the given Maths MCQs for Class 12 with Answers Chapter 1 Relations and Functions will help you. If you have any query regarding CBSE Class 12 Maths Relations and Functions MCQs Pdf, drop a comment below and we will get back to you at the earliest.

