The six trigonometric ratios are sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec). In geometry, trigonometry is a branch of mathematics that deals with the sides and angles of a right-angled triangle. Therefore, trig ratios are evaluated with respect to sides and angles.
The trigonometry ratios for a specific angle ‘θ’ is given below:
| Trigonometric Ratios | |
| Sin θ | Opposite Side to θ/Hypotenuse |
| Cos θ | Adjacent Side to θ/Hypotenuse |
| Tan θ | Opposite Side/Adjacent Side & Sin θ/Cos θ |
| Cot θ | Adjacent Side/Opposite Side & 1/tan θ |
| Sec θ | Hypotenuse/Adjacent Side & 1/cos θ |
| Cosec θ | Hypotenuse/Opposite Side & 1/sin θ |
Note: Opposite side is the perpendicular side and the adjacent side is the base of the right-triangle. Also, check out trigonometric functions to learn about each of these ratios or functions in detail.Trigonometric Identities
Definition
Trigonometric Ratios are defined as the values of all the trigonometric functions based on the value of the ratio of sides in a right-angled triangle. The ratios of sides of a right-angled triangle with respect to any of its acute angles are known as the trigonometric ratios of that particular angle.
The three sides of the right triangle are:
- Hypotenuse (the longest side)
- Perpendicular (opposite side to the angle)
- Base (Adjacent side to the angle)
How to Find Trigonometric Ratios?
Consider a right-angled triangle, right-angled at B.
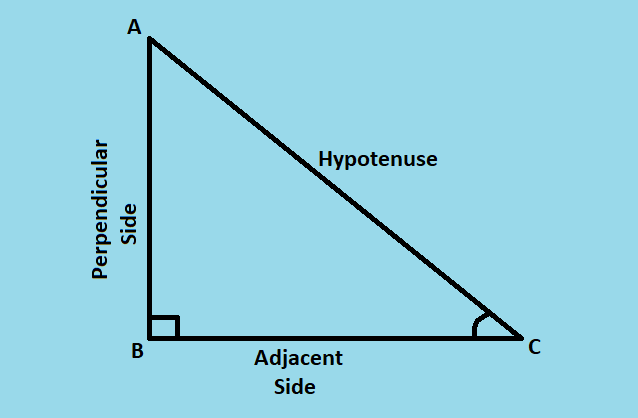
With respect to ∠C, the ratios of trigonometry are given as:
- sine: Sine of an angle is defined as the ratio of the side opposite(perpendicular side) to that angle to the hypotenuse.
- cosine: Cosine of an angle is defined as the ratio of the side adjacent to that angle to the hypotenuse.
- tangent: Tangent of an angle is defined as the ratio of the side opposite to that angle to the side adjacent to that angle.
- cosecant: Cosecant is a multiplicative inverse of sine.
- secant: Secant is a multiplicative inverse of cosine.
- cotangent: Cotangent is the multiplicative inverse of the tangent.
The above ratios are abbreviated as sin, cos, tan, cosec, sec and tan respectively in the order they are described. So, for Δ ABC, the ratios are defined as:
sin C = (Side opposite to ∠C)/(Hypotenuse) = AB/AC
cos C = (Side adjacent to ∠C)/(Hypotenuse) = BC/AC
tan C = (Side opposite to ∠C)/(Side adjacent to ∠C) = AB/AC = sin ∠C/cos ∠C
cosec C= 1/sin C = (Hypotenuse)/ (Side Opposite to ∠C) = AC/AB
sec C = 1/cos C = (Hypotenuse)/ (Side Opposite to ∠C) = AC/BC
cot C = 1/tan C = (Side adjacent to ∠C)/(Side opposite to ∠C)= BC/AB
In right Δ ABC, if ∠A and ∠C are assumed as 30° and 60°, then there can be infinite right triangles with those specifications but all the ratios written above for ∠C in all of those triangles will be same. So, all the ratios for any of the acute angles (either ∠A or ∠C) will be the same for every right triangle. This means that the ratios are independent of lengths of sides of the triangle.
Trigonometric Ratios Table
The trigonometric ratios for some specific angles such as 0 °, 30 °, 45 °, 60 ° and 90° are given below, which are commonly used in mathematical calculations.
| Angle | 0° | 30° | 45° | 60° | 90° |
| Sin C | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| Cos C | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| Tan C | 0 | 1/√3 | 1 | √3 | ∞ |
| Cot C | ∞ | √3 | 1 | 1/√3 | 0 |
| Sec C | 1 | 2/√3 | √2 | 2 | ∞ |
| Cosec C | ∞ | 2 | √2 | 2/√3 | 1 |
From this table, we can find the value for the trigonometric ratios for these angles. Examples are:
- Sin 30° = ½
- Cos 90° = 0
- Tan 45° = 1
Trigonometry Applications
Trigonometry is one of the most important branches of mathematics. Some of the applications of trigonometry are:
- Measuring the heights of towers or big mountains
- Determining the distance of the shore from the sea
- Finding the distance between two celestial bodies
- Determining the power output of solar cell panels at different inclinations
- Representing different physical quantities such as mechanical waves, electromagnetic waves, etc.
It is evident from the above examples that trigonometry has its involvement in a major part of our day-to-day life and much more. In most of the applications listed above, something was being measured and that is what trigonometry is all about.
Solved Problems
Q.1: If in a right-angled triangle ABC, right-angled at B, hypotenuse AC = 5cm, base BC = 3cm and perpendicular AB = 4cm and if ∠ACB = θ, then find tan θ, sin θ and cos θ.
Sol: Given,
In ∆ABC,
Hypotenuse, AC = 5cm
Base, BC = 3cm
Perpendicular, AB = 4cm
Then,
tan θ = Perpendicular/Base = 4/3
Sin θ = Perpendicular/Hypotenuse = AB/AC = ⅘
Cos θ = Base/Hypotenuse = BC/AC = ⅗
Q.2: Find the value of tan θ if sin θ = 12/5 and cos θ = ⅗.
Sol: Given, sin θ = 12/5 and cos θ = ⅗
As we know,
Tan θ = Sin θ/Cos θ
Tan θ = (12/5)/(⅗)
Tan θ = 12/3
Tan θ = 4
Practice Questions
- Find the value of sin θ, if tan θ = ¾ and cos θ = ½.
- Find tan θ if sin θ = 4/3 and cos θ = 3/2
- Find sec θ, if cos θ = 9/8
- Find cosec θ, if sin θ 16/5
